Abacus Exhibit in Rio Rancho, NM

Japanese 1:5 Soroban with kanji characters on the dividing bar representing denominations of yen.



Central Asian Schotty, 10-bead abacus



10-Bead school abacus of the kind Napoleon brought back to France from the 19th-century Russian campaign.



Here are the presentation foils included in the exhibit:






The following pages illustrate examples of abacus addition. First is how numbers are represented on the 1:4 soroban:



Next are two simple addition problems, the first one direct addition, the second using fives complements. But first I should explain the concept of "complements."

Since there are a limited number of beads on each rod, there are occasions when you can't directly add a quantity of beads. For numbers under 5, these problems are known as "fives complements." A five complement is a number that, when added to the original number, equals five. For example, the fives complements of 1,2,3 and 4 are: 4,3,2 and 1, respectively.

There are also tens complements of numbers: a number which, when added to the original number, equals ten. The tens complements of 1,2,3,4,5,6,7,8 and 9 are: 9,8,7,6,5,4,3,2 and 1, respectively.

The way that fives complements are used in addition is, instead of directly adding the number (which you can't, because there aren't enough beads left on the rod), you subtract the fives complement of the number and add a five bead from above the bar.

The way that tens complements are used in addition is, instead of directly adding the number (which you can't, because there aren't enough beads left on the rod), you subtract the tens complement of the number and add a single bead on the next rod to the left.



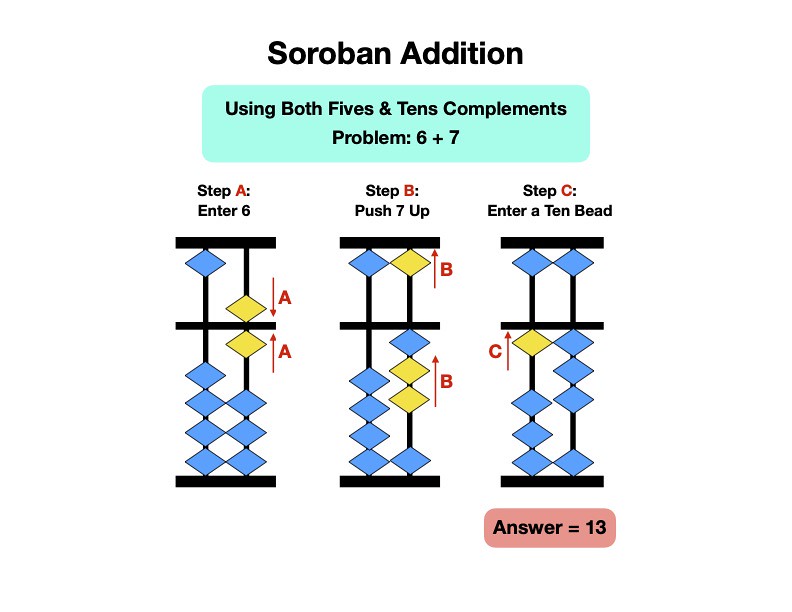
Next is a problem involving both fives and tens complements. These problems happen when you have to do a tens complement operation, but there aren't enough beads on the rod to subtract the tens complement. The shortcut method my Taiwanese abacus teacher taught was to "push the number up," as illustrated in the next foil, where in order to add 7 to 6, you "push the 7 up":



The photo below shows the classic book on Japanese soroban, by Takashi Kojima; that I first acquired in the early 1970s when I began my abacus journey. The photo is also accompanied by a contemporary Chinese-made teacher's abacus, designed so the beads stay put when hung vertically for the classroom:



A Brief Primer on Soroban Addition:

Performing addition and subtraction (the inverse of addition) efficiently on the soroban means quickly determining which kind of operation you need to perform. Though I'm not a master soroban operator, I can work my way around the beads well enough for my purposes, enough to know that I often can enter each number without consciously thinking how I did it, through rote practice. But I've since analyzed my methods, and have determined the following procedure for beginners to follow for addition on the beads. This procedure is based on Kojima's teachings, but expressed in logical steps for the western adult-brained learner.

Firstly, you do need to know the fives and tens complements.

Next are a series of questions you need to ask, in the order listed, when confronted with a single-digit addition problem:

A) Can the number be directly added? If yes: add the number, problem done. If no, go to step B.
(Examples of this kind of problem: 1 + 3 and 2 + 7)

B) Are both numbers less than five? If yes, subtract the five complement of the number and add a five bead (this is done with one swift downward move of the index finger), problem done. If no, go to step C.
(Examples of this kind of problem: 4 + 3 and 3 + 2)

C) Can the tens complement be directly subtracted? If yes, subtract the tens complement and add a bead on the next rod to the left, problem done. If no, go to step D.
(Examples of this kind of problem: 3 + 8 and 9 + 6)

D) Push the number up, then add a bead on the next rod to the left.
(Examples of this kind of problem: 5 + 9 and 7 + 6)

There is one more complication. Sometimes, when dealing with multi-digit numbers, when doing a tens complement problem and you need to add the single bead on the next rod to the left, if that rod already holds a value of either 4 or 9, you can't directly add that single bead. If the rod has a 4, you need to swipe down the five bead and all four ones beads (essentially doing a fives complement operation in order to add the single bead). If the rod has a value of 9, you have to clear the nine out and add the single bead to the next rod to its left.

I should also mention that when adding multi-digit numbers, you do so from left to right, like the order in which you would write or speak them. This is more efficient than the right-to-left paper method we were taught in school.

I know that for the rank beginner this all sounds complicated. But what I've described thus far is all you need to know to do addition problems involving numbers of any length. You do them one digit at a time, from left to right, using the rules I've described above.

Know also that I will be touching on this method in more depth in an upcoming video on my YouTube channel.