The Soroban Abacus Addition Method Explained
By now you know I've been an abacus aficionado for most of my adult life. Yet, despite the oddball nature of bead-frame calculators in the 21st century, I've met a number of people over the years who were actually interested enough in learning basic abacus addition to make an honest effort. Invariably, many of these adult learners would struggle with the concepts, never gain proficiency and eventually lose interest.
I was one of those adult learners who also struggled with some of the concepts, until I met a school teacher in Socorro, NM, a Taiwanese native and abacus user since her formative years, who showed me a few key concepts that made the Japanese soroban style of abacus much easier to use. In so doing I also noticed that the concept I struggled with was one she took for granted, having learned the soroban in her formative years, when the cerebral cortex is much more malleable. I soon realized that part of the problem was the nature of adult learners such as I.
My interest in the abacus waxes and wanes over the years, interspersed as it is with many other passions. Recently I've come to reconsider the problem of adult learners of the abacus, since I currently have an exhibit of my abacus collection on display at a local public library, and have been working to simplify the teaching of addition on the Japanese-style soroban.
The problem presented by the abacus is you have a limited number of beads available to represent numbers, thus when adding numbers together you frequently run out of beads, necessitating roundabout methods of completing the problem. I realized the seasoned abacus operator intuitively recognizes these various situations, on-the-fly, and immediately responds with the appropriate technique almost subconsciously, through rote training. What I immediately set about doing was documenting those various instances when alternative techniques are required to complete a calculation, with the goal of systematizing a formal methodology for approaching any addition problem.
Naturally charts and graphs would be employed, as I can imagine Arlo Guthrie explaining in his classic piece Alice's Restaurant Massacree: "...twenty-seven 8-by-10 color glossy pictures with circles and arrows and a paragraph on the back of each one explaining what each one was, to be used as evidence against us..." So be forewarned about the color glossy pictures ahead!
As I said, I've been using the abacus for years, with proficiency sufficient for basic addition, and thus I had to slowly unravel my thinking process of how I approach these problem situations. I started by mapping all of the possible addition problems and color-coding them with their requisite solution technique.
Figure One: Addition problems on the soroban require four general categories of response. The first category, where the cells in the above chart are white, are direct-entry problems where no special technique is needed. Simply enter the starting number (indicated by numbers along the left column of the chart) and then enter the addend (indicated by numbers along the top of the chart) and the answer presents itself on the soroban.
Here, these direct-entry problems have been isolated from the rest of the cells:
Figure Two: The second category of problem response are when adding numbers together that are both less than five, but there aren't enough beads on that rod to complete the problem. These are indicated by the cells highlighted in yellow, and marked with a "5" in Figure One. These cells are isolated in Figure Three, below. The solution of these problems require the employment of what are termed "fives complements."
Figure Three: The use of complementary numbers is a technique designed to get around the problem of running out of beads to complete a calculation. Instead of adding the number, we subtract its complement and add the next higher bead. Consider the following table in Figure Four:
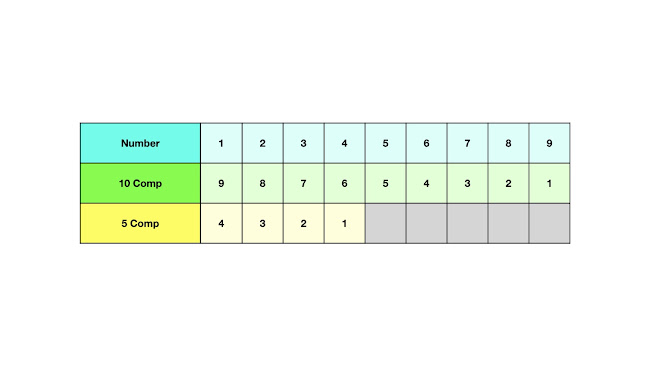
Figure Four:
The top row lists the digits 1 through 9, and the following two rows list the tens complements and fives complements of each number, respectively. The five complement of a number is a number that, when added to the original number, equals five. Similarly, the ten complement of a number is a number that, when added to the original number, equals ten. It is a requirement that the abacus operator know by heart both the fives and tens complements.
So, in this second category of problem the solution is found by adding a five bead to the rod and subtracting the fives complement of the number, in one swift downward motion of the index finger.
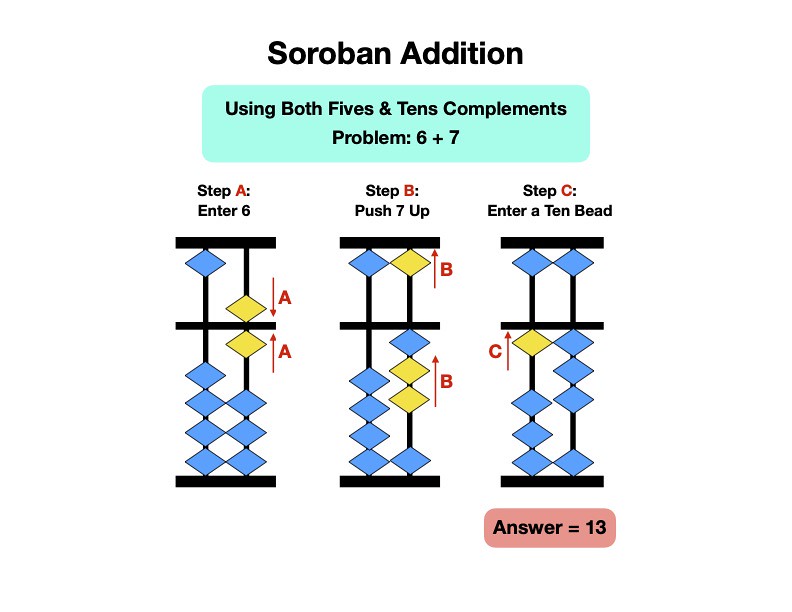
The third category of problem response are those whose solution is found by employing a tens complement operation, as indicated by the green cells in Figure One. With these problems, the tens complement of the addend are subtracted from the rod, then a single ("ten") bead is added on the next rod to its left. These problems have been isolated in the chart in Figure Five, below:
Figure Five: There is a fourth category of response, indicated by the rose colored cells in Figure One, and isolated in Figure Six, below. These kinds of problems were the ones that I stumbled to understand, as they are ostensibly tens complements problems but require a fives complement operation to also be performed; what I call "nested" or "combined" complements problems.
Figure Six: The shortcut method my abacus teacher taught me for solving these kinds of problems was to "push up" the number, then add the single ("ten") bead on the rod to the immediate left (instead of thinking of it as a fives complement problem nested within a tens complement problem).
In addition to categorizing the soroban abacus operations into four categories of response, I had to decipher in what order I tend to solve them in my mind; since I often solve the simpler problems automatically, with little conscious thought. In so doing I devised a checklist, in the form of three questions I use to interrogate a problem, resulting in the four possible response methods.
Figure Seven: By following this checklist in the order suggested, the simplest solutions are arrived at first, followed by solution methods of increased complexity. I've found that following this sequence of questions always leads to a solution every time, but there are two additional complexities to unravel before we can call this bulletproof.
The last two solution methods involve tens complement operations, where a single ("ten") bead is added on the next rod to its left. However, there are two situations where that single ten bead cannot be entered.
Figure Eight: As you can see from Figure Eight, above, if the rod to the immediate left of our problem is either a four or a nine, there will be insufficient beads available to complete a tens complement operation. In the case of a four, all the beads on that rod are lowered, while in the case of a nine, that rod is cleared and the single bead is added to the next rod to its left.
This is essentially all that one needs to know in order to master addition on the soroban. However, there are a few things I've left out, assuming you already knew them. The first is how numbers are entered. The abacus is "cleared" when the top and bottom beads are pushed away from the dividing bar. Numbers are entered when they are pushed toward the dividing bar. The four beads below the bar are each worth one point, while the single bead above the bar is worth five points.
Secondly, numbers are entered on various rods in place-value fashion, similar to how numbers are written on paper. For addition, multidigit numbers are summed from left to right instead of the more usual right to left. When adding multidigit numbers, each digit is treated as a separate single-digit problem, using the rules outlined above.
Finally, proficiency is only gained through constant practice. One easy practice method is summing the number sequence 123,456,789 ten times. In the process, every possible combination of addition problem will be encountered. You can easily tell if you've arrived at the correct answer because it should be: 1,234,567,890. This lengthy number should be compatible with any soroban having at least ten rods.
You can also use your grocery store and shopping receipts as another kind of practice problem. Add up the prices listed on your receipts and they should match the store's subtotal. This is a good way to bring some fun into the drudgery of shopping, as you look forward to adding up the receipt totals afterwards.
I've presented these techniques in a comprehensive video, embedded at the top of this article. My intent is, by following this method, addition on the soroban can be mastered by the average adult learner with but rote practice to gain proficiency and speed. I hope you will consider becoming an abacus practitioner.
Post-Script: I'm frequently asked for links where people can buy a soroban-style abacus at a reasonable price. Keeping in mind that artisanally-crafted Japanese soroban are works of art and their construction methods an official national treasure, I've found some inexpensive Chinese-made versions with beads sufficiently large for the adult westerner. Here is one such example: www.shorturl.at/tvwM8
Labels: Abacus Soroban